408 代码题学习笔记
心路历程:
- -> 这还可以接受
- -> 这东西好像得背一背
- -> 这是个数学题
- -> 这是玄学
- -> 狗东西压根没想让我写出来 😡
1. 顺序表
1.1. 顺序表的定义
1.1.1. 静态定义顺序表
c
#define MaxSize 100
typedef struct SqList{
int data[MaxSize];
int length;
} SqList;
SqList L;
L.data[0] = 0;1.1.2. 动态定义顺序表
c
typedef struct {
int *data;
int MaxSize,length;
} SqList;
SqList L2;
L2.data = (int*)malloc(sizeof(int)*L2.MaxSize);
L2.data[0] = 1;1.2. 顺序表的遍历
c
void ListVisit(SqList L){
if(L.length == 0){
return;
}
for(int i = 0; i < L.length; i++){
printf("%d", L.data[i]);
}
}1.3. 假设有一个顺序表 L, 请设计一个算法,查找顺序表 L 中第一个值为 x 的元素,若查找成功,则返回其位序,若查找失败,则返回 0。
c
int Search_X(SqList L,int x){
if(L.length == 0){
return 0;
}
for(int i = 0; i < L.length; i++){
if(x == L.data[i]){
return i+1;
}
}
return 0;
}1.4. 假设有一个顺序表 L, 其存储的所有数据元素均为非 0 整数,请设计一个算法,查找 L 中第 i 个元素并返回其值。
c
int Search_I(SqList L, int i){
if(L.length == 0){
return 0;
}
// 合法
if(i <= L.length && i > 0){
return L.data[i-1];
}
// 非法
return 0;
}1.5. 假设有一个顺序表 L, 请设计一个算法,在 L 的第 i 个位置插入新元素 x。若不能正常插入,则返回 false, 表示插入失败;若能够正常插入,则在顺序表 L 中的第 i 个位置插入新元素 x, 返回 true, 表示插入成功。
c
bool ListInsert(SqList &L,int i,int x){ // 改变L需要加&
if(i < 1 || i>L.length || L.MaxSize == L.length){
return false;
}
// 从后往前遍历
for(j = L.length;j >= i; j--){
L.data[j] = L.data[j-1];
}
L.data[i-1] = x;
L.length++;
return true;
}1.6. 假设有一个非空顺序表 L, 其中的元素非递减有序排列,请设计一个算法在插入元素 x 后保持该顺序表仍然非递减有序排列,假设插入操作肯定成功,插入成功后返回插入元素所在位置。
c
int ListInsert(SqList &L, int x){
int i;
for(i = L.length; i > 0 && L.data[i-1]>=x; i--){
L.data[i] = L.data[i-1];
}
L.data[i+1] = x;
L.length++;
return i+1;
}另有
c
int ListInsert(SqList &L, int x){
int i;
// 找到插入位置i
for(i = 0; i < L.length; i++){
if(L.data[i] > x){
break;
}
}
// 移动i+1后面的元素
for(int j = L.length; j>=i+1; j--){
L.data[j] = L.data[j-1];
}
return i;
}1.7. 删除顺序表 L 中第 i 个位置的元素,若删除失败,则返回 false; 若删除成功,则将被删元素的值赋给引用参数 x, 然后返回 true。
c
bool Delete_I(SqList &L, int &x, int i){
if(L.length == 0 || i < 1 || i > L.length){
return false;
}
x = L.data[length-1];
for(int j = i; j < L.length; j++){
L.data[j-1] = L.data[j];
}
L.length--;
return true;
}1.8. 假设有一个顺序表 L, L 有最小值且最小值唯一,请设计一个算法删除 L 中的最小值元素并由函数返回被删元素的值。
c
int Delete_min(SqList &L){
int min = L.data[0]; // 最小值是谁
int pos = 0; // 初始位置是哪
for(int i = 1; i < L.length; i++){
if(min > L.data[i]){
min = L.data[i];
pos = i;
}
}
for(int j = pos; j < L.length; j++){
L.data[j] = L.data[j+1];
}
L.length--;
return min;
}1.9. 假设有一个顺序表 L, 请编写一个时间复杂度为 O(以、空间复杂度为 O(1)的算法,删除顺序表 L 中所有值为 x 的元素。
c
// 排队法
void Del_x(SqList &L,int x){
if(L.length == 0){
return;
}
int j = 0;
for(int i = 0;i <= L.length;i++){
if(L.data[i] != x){
L.data[j] = L.data[i];
j++;
}
}
L.length = j;
}1.10. 假设有一个顺序表 L, 请设计一个算法删除 L 中元素值在给定值 s 与 t 之间(包含 s 和 t, 要求 s < t)的所有元素,若顺序表为空或给定的 s 和 t 值不合理,则返回 false, 若执行成功则返回 true。
c
// 计数法
bool Delete_Between(SqList &L, int s, int t){
if(L.length == 0 || s >=t || s < 1 || t >= L.length){
return false;
}
int p = 0;
for(int i = 0; i >= 0; i++){
if(L.data[i] >= s && L.data[i] <= t){
p++;
}else {
L.data[p] = L.data[i];
}
}
L.length = L.length - p;
return true;
}1.11. 请设计一个算法,在一个有序顺序表中删除所有值重复的元素,使该顺序表中所有元素的值均不同
c
void Del_Iterate(SqList &L){
if(L.length <= 1){
return;
}
int j = 1;
for(int i = 1; i < L.length; i++){
if(L.data[i] != L.data[i-1]){
L.data[j] = L.data[i];
}
}
L.length = j;
}1.12. 请设计一个算法,在一个无序顺序表中删除所有值重复的元素,使该顺序表中所有元素的值均不同且删除后的元素间相对位置保持不变。
c
// 排队法
void Del_Iterate(SqList &L){
if(L.length <= 1){
return;
}
int k = 1; // 新顺序表的长度
int j; // 让第一层循环能够获取j
for(int i = 1; i <= L.length; i++){
for(j = 1; j < i; j++){
if(L.data[i] == L.data[j]){
break; // 停止比较
}
}
if(j == i){ // 没有重复值
L.data[k] = L.data[i]; // 重排
k++;
}
}
L.length = k;
}1.13. 请设计一个尽可能高效的算法,将顺序表 L 中的所有元素逆置,要求算法的空间复杂度为 O(1)
c
void Reverse(SqList &L){
if(L.length == 0){
return;
}
for(int i = 0,j = L.length - 1; i < j; i++,j--){ // 定义双变量
temp = L.data[i];
L.data[i] = L.data[j];
L.data[j] = temp;
}
}1.14. 已知一个一维数组 A [m+n] 中依次存放了两个线性表(a1, a2,…, am)和(b1, b2,…, bn), 请设计一个算法,将数组中的两个线性表位置互换,即设计一个算法将原数组(a1, a2,…, am, b1, b2,…, bn)变为(b1, b2,…, bn, a1, a2,…, am)。
法一:
c
void Swap(int A[], int m, int n){
int B[m+n];
for(int i = 0; i < m+n; i++){
B[i] = A[i];
}
for(int i = m; i < m+n; i++){
A[i - m] = B[m];
}
for(int i = 0; i < m; i++){
A[i + m] = B[i];
}
}法二:
c
// 三次逆置,无辅助数组
void Reverse(int A[], int low, int high){
int temp;
for(int i = low, j = high; i < j; i++,j--){
temp = A.data[i];
A.data[i] = A.data[j];
A.data[j] = temp;
}
}
void Swap(int A[], int m, int n){
Reverse(A[], 0, m-1);
Reverse(A[], m, m+n-1);
Reverse(A[], 0, m+n-1);
}1.15. 现有两个非递减有序的顺序表 A 和 B, 请设计一个算法,将两个顺序表 A 和 B 合并为一个新的 非递减 有序顺序表 C。
c
// 这是题目给出的表的结构
typedef struct {
int *data;
int length,MaxSize;
} SqlList;
void Merge(SqlList A, SqList B, SqList &C){
if(A.length == 0 && B.length == 0 || A.length+B.length > C.MaxSize){
return false;
}
int i=0,j=0,k=0; // 循环变量
while(i < A.length && j < B.length){
if(A.data[i] <= B.data[j]){
C.data[k] = A.data[i];
k++;
i++;
}else {
C.data[k] = B.data[j];
k++;
j++;
}
}
while(i < A.length){
C.data[k] = A.data[i];
k++;
i++;
}
while(j < B.length){
C.data[k] = B.data[j];
k++;
j++;
}
C.length = k;
return true;
}1.16. 现有两个非递减有序的顺序表 A 和 B, 请设计一个算法,将两个顺序表 A 和 B 合并为一个新的 非递增 有序顺序表 C。
c
void Merge(SqlList A, SqList B, SqList &C){
if(A.length == 0 && B.length == 0 || A.length+B.length > C.MaxSize){
return false;
}
int i = A.length - 1;
int j = B.length - 1;
int k = 0;
while(i >=0 && j >=0){
if(A.data[i] >= B.data[j]){
C.data[k] = A.data[i];
k++;
i--;
}else {
C.data[k] = B.data[j];
k++;
j--;
}
}
while(i >= 0){
C.data[k] = A.data[i];
k++;
i--;
}
while(j >= 0){
C.data[k] = B.data[j];
k++;
j--;
}
C.length = k;
return true;
}1.17. 给定三个序列 A、B、C, 三个序列的长度均 n 为且每个序列都是递增的,请设计一个时间上尽可能高效的算法,逐行输出同时存在于这三个序列中的所有元素。例如,数组 A 为{4,2,3,6},数组 B 为{-5,0,2,6},数组 C 为{1,2,4,6},则逐行输出 2 和 6。
c
// 暴力解就是3个for循环
// ...
//较小值向较大值靠拢
int max(int A, int B, int C){
int max;
if(A > B){
max = A;
} else {
max = B;
}
if(max > C){
return max;
} else {
return C;
}
}
void PrintSame(int A[], int B[], int C[]){
int i=0,j=0,k=0;
int m;
while(i<A.length && j<B.length && k<C.length){
if(A.data[i] == B.data[j] && A.data[i] == C.data[k]){
printf("%d/n",A.data[i]);
}
m = max(A.data[i],B.data[j],C.data[k])
if(A.data[i]<m){
i++;
}
if(B.data[j]<m){
j++;
}
if(C.data[k]<m){
k++;
}
}
}2. 链表
2.1. 单链表的结构体定义
c
typedef struct LNode{
int data;
struct LNode *next;
} LNode,*LinkList;
// struct LNode -> Lnode
// struct LNode* -> LinkList
// LinkList p -> LNode *p
// 带头结点
void InitList1(LinkList &L){
L = (LinkList)malloc(sizeof(LNode));
L->next = NULL;
}
bool IsEmptyList1(LinkList L){
if(L->next == NULL){
return true;
}else {
return false;
}
}
// 不带头结点
void InitList2(LinkList &L){
L = NULL;
}
bool IsEmptyList2(LinkList &L){
if(L == NULL){
return true;
}else {
return false;
}
}
// 注:链表不存在L.data之类操作2.2. 遍历输出单链表 L 中的值
c
void LNodeList(LinkList L){
if(L->next == NULL){
return;
}
LNode *p = L->next;
while(p != NULL){
printf("%d",p->data);
p = p->next;
}
}2.3. 请设计一个算法,查找一个带头结点的单链表 L 中第 i 个数据结点的位置,若存在,则返回指向该结点的指针,若不存在,则返回 NULL
c
LNode *Search_i(LinkList L, int i){
if(L->next == NULL || i < 1){ // 判空
return;
}
LNode *p = L->next;
int k = 1;
while(p != NULL){
if(i = k){
return p;
}
p = p->next;
k++;
}
return NULL; // 说明 i 太大了
}2.4. 计算带头结点的单链表 L 中数据结点的个数。
c
int DataNum(LinkList L){
if(L->next == NULL){
return 0;
}
LNode *p = L->next;
int k = 0;
while(p != NULL){
p = p->next;
k++;
}
return k;
}2.5. 在一个带头结点的非递减有序单链表中插入一个值为 x 的新结点,使得插入新结点后链表依然非递减有序
c
void InsertList(LinkList &L, int x){
LNode *p = L->next, *pre = L;
while(p != NULL){
if(p->data > x){
break;
}
pre = p;
p = p->next;
}
LNode *s = (LNode*)malloc(sizeof(LNode));
s->data = x;
s->next = p;
pre->next = s;
}2.6. 采用头插法在头指针 L 处建立一个带头结点的单链表,输入-1 表示结束,头插结束后返回建立的单链表。
c
LinkList HeadInsert(LinkList &L){
L = (LinkList)malloc(sizeof(LNode));
L->next = NULL;
LNode *x
int i;
scanf("%d",&i);
while(i != -1){
x = (*LNode)malloc(sizeof(LNode));
x->data = i;
x->next = L->next;
L->next = i;
scanf("%d",&i);
}
return L;
}2.7. 采用尾插法在头指针 L 处建立一个带头结点的单链表,输入-1 表示结束,尾插结束后返回建立的单链表。
c
LinkList TailInsert(LinkList &L){
L = (LinkList)malloc(sizeof(LNode));
LNode *r = L; // 尾指针
LNode *s;
int x;
scanf("%d",&x);
while(x == -1){
s = (LNode*)malloc(sizeof(LNode)) // 为结点分配内存空间
s->data = x;
r->next = s;
r = s;
scanf("%d", &x);
}
r->next = NULL; // 尾结点的next指针置空
return L;
}2.8. 试编写算法将一个带头结点的单链表 L 就地逆置,所谓“就地”是指空间复杂度为 O(1)。
C
void Reverse(LinkList &L){
if(L->next == NULL){
return;
}
LNode *p = L->next,*r;
L->next = NULL; // 将尾结点next置空
while(r->next = NULL){
r = p->next; // 防断链指针
p->next = L->next;
L->next = p;
p = r;
}
}2.9. 将一个带头结点的单链表 A 分解为两个带头结点的单链表 A 和 B, 使得 A 表中含有原表中位序为奇数的结点,B 表中含有原表中位序为偶数的结点,且保持结点间相对顺序不变,最后返回 B 表,
c
LinkList Reverse(LinkList &L){
if(L->next = NULL){
return NULL;
}
LinkList B = (LinkList)malloc(sizeof(LNode));
LNode *p = A->next;
LNode *ra = A,*rb = B;
while(p != NULL){
ra->next = p;
ra = p;
p = p->next;
if(p != NULL){ // 单链表奇数或偶数
rb->next = p;
rb = p;
p = p->next;
}
}
ra->next = NULL; // 尾指针置空
rb->next = NULL;
}2.10. 编写算法将一个带头结点的单链表 A ={a1, b1, a2, b2,..., an, bn}分解为两个带头结点的单链表 A 和 B 使得 A ={a1, a2,…, an}, B ={bn,…, b2, b1}, 原 A 表中结点个数不一定为偶数。
c
// 对A使用尾插法(正序),对B使用头插法(逆序)
LinkList Split(LinkList A){
if(A->next == NULL){
return NULL;
}
LinkList B = (LNode *)malloc(sizeof(LNode));
B->next = NULL;
LNode *p = A->next,*r = A,*q;
while(p != NULL){
r->next = p;
r = p;
p = p->next;
while(p != NULL){
q = p->next; // 防断链指针
p->next = B->next;
B->next = p;
p = q;
}
}
r->next = NULL;
return B;
}2.11. 将一个带头结点的单链表 L 分解为两个带头结点的单链表 A 和 B, 使得 A 表中含有原表中数据域为奇数的结点,而 B 表中含有原表中数据域为偶数的结点,且保持相对顺序不变,最后删除单链表 L 的头结点。
c
void Split(LinkList L,LinkList &A,LinkList &B){
if(L->next == NULL){
return;
}
// 分配空间
A = (LinkList)malloc(sizeof(LNode));
B = (LinkList)malloc(sizeof(LNode));
// 定义指针
LNode *p = L->next,*ra = A,*rb = B;
while(p != NULL){
if(p->data % 2 != 0){
ra->next = p;
ra = p;
}else{
rb->next = p;
rb = p;
}
p = p->next;
}
ra->next = NULL;
rb->next = NULL;
free(L);
}2.12. 有一个带头结点单链表 L,L 中各个结点的值都不相同,请设计一个算法,删除链表 L 中的最小值结点。
c
void Del_Min(LinkList L){
if(L->next == NULL){
return;
}
LNode *minpre = L,*minp = L->next;
LNode *pre = L->next,*p = pre->next;
while(p != NULL){
if(p->data < minp->data){
minp = p;
minpre = pre;
}
pre = p;
p = p->next;
}
minpre->next = minp->next;
free(minp);
}2.13. 请设计一个算法,在带头结点的单链表 L 中删除所有值为 x 的结点,并释放其空间。
c
void Del_x(LinkList L, int x){
if(L->next == NULL){
return;
}
LNode *pre = L,p = L->next;
while(p != NULL){
if(p->data = x){
pre->next = p->next;
free(p);
p = pre->next;
}else{
pre = p;
p = p->next;
}
}
}2.14. 请设计一个算法,在带头结点的单链表 L 中删除所有数据域的值介于给定的两个值之间的结点,并释放其空间。
c
void Del_min_max(LinkList L,int min,int max){
if(L->next == NULL || min >= max){
return;
}
LNode *pre = L,*p = L->next;
while(p != NULL){
if(p->data >= min && p->data <= max){
pre->next = p->next;
free(p);
p = pre->next;
}else{
pre = p;
p = p->next;
}
}
}2.15. 请设计一个算法,在带头结点的非递减有序单链表 L 中删除所有值重复的结点,使值重复的结点只保留一个。
c
void Del_Same(LinkList L){
if(L->next == NULL){
return;
}
LNode *pre = L->next,*p = pre->next;
while(p != NULL){
if(pre->data == p->data){
pre->next = p->next;
free(p);
p = pre->next;
}else{
pre = p;
p = p->next;
}
}
}2.16. 请设计一个算法,在带头结点的无序单链表 L 中删除所有值重复的结点,使值重复的结点只保留一个
c
void Del_Same(LinkList L){
if(L->next == NULL){
return;
}
LNode *r = L->next;
LNode *pre,*p;
while(r!=NULL){
pre = r; // 每次r=r->next都会对p和pre赋值
p = r->next;
while(p!=NULL){
if(p->data == r->data){
pre->next = p->next;
free(p);
p = pre->next;
}else{
pre = p;
p = p->next;
}
}
r = r->next;
}
}2.17. 设 A 和 B 是两个带头结点的递增有序单链表,请设计一个算法,求单链表 A 与 B 的交集,并生成一个新的单链表 C, 要求不破坏 A、B 的结点。
c
LinkList Union_Same(LinkList A,LinkList B){
if(A->next == NULL || B->next == NULL){
return NULL;
}
LinkList C = (LinkList)malloc(sizeof(LNode));
LNode *p = A->next,*q = B->next,*r = C; // 遍历指针
LNode *s; // 存结点
while(p != NULL && q != NULL){
if(p->data > q->data){
q = q->next;
}else if(p->data < q->data){
p = p->next;
}else{
s->data = p->data;
r->next = s;
r = r->next;
p = p->next;
q = q->next;
}
}
r->next = NULL;
return C;
}2.18. 设 A 和 B 是两个带头结点的递增有序单链表,请设计一个算法,求单链表 A 与 B 的交集,并存放于 A 链表中,其它结点均释放其空间。
c
LinkList Union_Same(LinkList A,LinkList B){
if(A->next == NULL || B->next == NULL){
return NULL;
}
LNode *p = A->next,*q = B->next,*r = A;
LNode *u;
while(p != NULL && q != NULL){
if(p->data > q->data){
u = q->next;
free(q);
q = u;
}else if(p->data < q->data){
u = p->next;
free(p);
p = u;
}else{
r->next = p;
p = p->next;
u = q->next;
free(q);
q = u;
}
}
while(p != NULL){
u = p->next;
free(p);
p = u;
}
while(q != NULL){
u = q->next;
free(q);
q = u;
}
r->next = NULL; // 尾指针置空
free(B); // 释放头结点
return A;
}2.19. 设 A 和 B 是两个带头结点的递增有序单链表,请设计一个算法,将 A 和 B 两个单链表归并为一个带头结点的非递减有序单疑表,要求利用原来两个单链表的结点组成归并后的单链表。
c
LinkList Merge(LinkList A,LinkList B){
if(A->next == NULL && B->next = NULL){
return NULL;
}
LNode *p = A->next,*q = B->next,*r = A;
while(p != NULL && q != NULL){
if(p.data >= q.data){
r->next = q;
r = q;
q = q->next;
}else{
r->next = p;
r = p;
p = p->next;
}
}
while(p->next != NULL){
r->next = p;
r = p;
p = p->next;
}
while(q->next != NULL){
r->next = q;
r = q;
q = q->next;
}
r->next = NULL;
free(B);
return A;
}2.20. 设 A 和 B 是两个带头结点的递增有序单链表,请设计一个算法,将 A 和 B 两个单链表归并为一个带头结点的非递增有序单链表,要求利用原来两个单链表的结点组成归并后的单链表。
c
LinkList Merge(LinkList A,LinkList B){
if(A->next == NULL && B->next ==NULL){
return;
}
LNode *p = A->next,*q = B->next,*r;
A->next = NULL;
while(p != NULL && q != NULL){
if(p->data >= q->data){
r = q->next;
q->next = A->next;
A->next = q;
q = r;
}else{
r = p->next;
p->next = A->next;
A->next = p;
p = r;
}
}
while(p->next != NULL){
r = p->next;
p->next = A->next;
A->next = p;
p = r;
}
while(q->next != NULL){
r = q->next;
q->next = A->next;
A->next = q;
q = r;
}
free(B);
return A;
}2.21. 设 A 和 B 是两个带头结点的递增有序单链表,请设计一个算法,求单链表 A 与 B 的差集,并返回差集链表。链表 A 与 B 的差集定义为:在链表 A 中存在但不在链表 B 中存在的所有结点的集合。要求利用原来两个单链表的结点组成差集链表,其它结点均释放其空间。
c
LinkList Diff(LinkList A,LinkList B){
if(A->next == NULL || B->next == NULL){
return NULL;
}
LNode *p = A->next,*q = B->next,*r = A;
LNode *u;
while(p != NULL && q != NULL){
if(p->data < q->data){
r->next = p;
p = p->next;
}else if(p->data > q->data){
u = q->next;
free(q);
q = u;
}else{
u = p->next;
free(p);
p = u;
u = q->next;
free(q);
q = u;
}
}
while(p->next != NULL){
r->next = p;
p = p->next;
}
while(q->next != NULL){
u = q->next;
free(q);
q = u;
}
r->next = NULL;
free(B);
return A;
}2.22. 两个整数序列 A ={a1, a2, a3,…, am}和 B ={b1, b2, b3,…, bn}已经存入两个带头结点的单链表中请设计一个算法,判断序列 B 是否是序列 A 的连续子序列。
c
bool Pattern(LinkList A,LinkList B){
LNode *p = A->next,*q = B->next,*r = A;
LNode *u;
while(p != NULL && q != NULL){
if(p->data == q->data){
p = p->next;
q = q->next;
}else{
pre = pre->next;
p = pre;
q = B->next;
}
}
if(q == NULL){
return true;
}else{
return false;
}
}2.23. 通常单链表尾结点指针域为 NULL, 而单链表有环,是指单链表最后一个结点的指针指向了链表中的某个结点。请设计一个算法,判断一个带头结点的单链表 L 是否有环,如果有环,返回环的入口结点位置,如果没有,返回 NULL。
c
// 有环无环:快慢指针问题 找到相遇点:数学问题 -> a=nr-x
LinkList FindLoop(LinkList L){
if(L->next == NULL){
return NULL;
}
LNode *slow = L,*fast = L;
while(fast != NULL || fast->next != NULL){
if(fast != slow){
fast = fast->next->next;
slow = slow->next;
}else{
break;
}
}
LNode *p = L;
LNode *q = slow;
while(p != q){
p = p->next;
q = q->next;
}
return p;
}2.24. 有两个带头结点的非空循环单链表 h1 和 h2, 请设计一个算法,将链表 h2 链接到链表 h1 之后,要求链接后的链表仍是一个带头结点的循环单链表。
c
LinkList Link(LinkList h1,LinkList h2){
LNode *p = h1->next,*q = h2->next;
while(p->next != h1){
p = p->next;
}
while(q->next != h2){
q = q->next;
}
p->next = h2->next;
q->next = h1;
free(h2);
}2.25. 有一个带头结点的循环单链表 L, 链表 L 中含有三类字符的数据元素(如:字母字符、数字字符和其它字符),请设计一个算法,将链表拆分为三个不带头结点的循环单链表,其中每个循环单链表均只含一类字符。
c
void Split(LinkList L, LinkList &A, LinkList &B, LinkList &C){
A = (LinkList)malloc(sizeof(LNode));
B = (LinkList)malloc(sizeof(LNode));
C = (LinkList)malloc(sizeof(LNode));
LNode *p = L->next,*ra = A,*rb = B,*rc = C;
while(p->next != L){
if(p->data > 'a' && p->data < 'z' || p->data > 'A' && p->data < 'Z'){
ra->next = p;
ra = ra->next;
}else if(p->data > '0' && p->data < '9'){
rb->next = p;
rb = rb->next;
}else{
rc->next = p;
rc = rc->next;
}
p = p->next;
}
ra->next = A;
rb->next = B;
rc->next = C;
free(L);
}2.26. 有一个不带头结点的单链表 L, L 中各个结点的值都不相同,请设计一个算法,删除链表 L 中的最小值结点。
法一:
c
void Del_Min(LinkList &L){
if(L == NULL){
return;
}
LNode *pre,*p = L;
LNode *premin,*minp = L;
while(p != NULL){
if(p->data < minp->data){
minp = p;
minpre = pre;
}
pre = p;
p = p->next;
}
if(minp == L){
L = L->next;
free(minp);
}else{
minpre->next = minp->next;
free(minp);
}
}法二:
c
void Del_Min(LinkList &L){
if(L == NULL){
return;
}
LinkList head = (LinkList)malloc(sizeof(LNode));
head->next = L;
LNode *p = L,*pre = head;
LNode *minp = p,*premin = pre;
while(p != NULL){
if(p->data <= minp->data){
minp = p;
minpre = pre;
}
pre = p;
p = p->next;
}
minpre->next = minp->next;
free(minp);
L = head->next;
free(head);
}2.27. 设将 n(n > 1)个整数存放到不带头结点的单链表 L 中,设计算法将 L 中保存的序列循环右移 k(0 < k < n)个位置。例如,若 k = 1, 则将链表{0,1,2,3}变为{3,0,1,2}。
c
LinkList Move_k(LinkList L,int k){
LNode *p = L;
int len = 1;
while(p->next != NULL){
p = p->next;
len++;
}
p->next = L;
for(int i = 0;i < len-k;i++){
p = p->next;
}
L = p->next;
p->next = NULL;
return L;
}2.28. 设有一个不带头结点的长度为(n 为偶数)的非空单链表,且结点值都大于 0,设计算法求这个单链表的最大孪生和。孪生和定义为二个结点值与其孪生结点值之和,对于第 i 个结点(从 0 开始)其孪生结点为第 n-i-1 个结点。
c
// 快慢指针法
int Sum_Max(LinkList L){
LNode *slow = L,*fast = L;
while(fast->next != NULL){
slow = slow->next;
fast = fast->next->next;
}
// 将后半部分逆置
LNode *p = slow->next,*q; // q是防断链指针
slow->next = NULL;
while(q != NULL){
q = p->next;
p->next = slow->next;
slow->next = p;
}
p = L;
q = slow->next;
int max = p->data + q->data;
while(q != NULL){
if((p->data + q->data) > max){
max = p->data + q->data;
}
p = p->next;
q = q->next;
}
return max;
}2.29. (约瑟夫环)有 n 个人围成一个圈,他们的编号为 1~n。现在要求从第 1 个人开始报数,数到 m 的人出列,出列后的下一个人继续从 1 开始报数,同样数到 m 的人出列,一直重复此过程,直到圈中只剩下最后一个人,返回其编号。
c
int Joesphus(LinkList L,int m){
// 初始化指针
LNode *p = L,*q = L;
while(q->next != L){
q = q->next;
}
while(p->next != p){
for(int i = 1; i < m; i++){
pre = p;
p = p->next;
}
pre->next = p->next;
free(p);
p = pre->next;
}
return p->data;
}2.30. 双链表的结构体定义。
c
typedef struct DNode{
int data;
struct DNode *prior,*next;
} DNode, *DLinkList;2.31. 在一个带头结点的非递减有序双链表中插入一个值为 x 的新结点,使得插入新结点后链表依然非递减有序。
c
void ListInsert(LinkList L, int x){
DNode *p = L->next,*pre = L;
while(p->data < x){
pre = p;
p = p->next;
}
DNode *s = (DNode *)malloc(sizeof(DNode));
s->data = x;
s->prior = pre;
pre->next = s;
s->next = p;
if(p != NULL){ // 新插入的结点后面可能为空
p->prior = s;
}
}2.32. 有一个带头结点的双链表 L, L 中各个结点的值都不相同,请设计一个算法,删除链表 L 中的最小值结点。
c
void Del_Min(DLinkList L){
DNode *p = L->next,*pre = L;
DNode *minp = L->next,*minpre = L;
while(p != NULL){
if(p->data < minp->data){
minp = p;
}
pre = p;
p->next;
}
minpre->next = minp->next;
if(minp->next != NULL){
minp->next->prior = minpre;
}
free(minp);
}2.33. 请设计一个算法,判断带头结点的循环双链表 L 是否对称
c
bool Asymmetries(DLinkList L){
if(L->next == L || L->next->next == L){
return false;
}
DNode *p = L->next,*q = L->prior;
while(p != q && q->next != p){
if(p->data == q->data){
p = p->next;
q = q->next;
}else{
return false;
}
}
return true;
}2.34. 有一个带头结点的双链表 L, L 中各个结点的值都不相同,请设计一个算法,将链表 L 中的最大值结点移动到最前面。
c
void Move_Max(DLinkList L){
if(L->next == NULL){
return;
}
DNode *pre = L,*p = L->next;
DNode *maxp = p,*maxpre = pre;
while(p != NULL){
if(p->data > maxp->data){
maxp = p;
maxpre = pre;
}
pre = p
p = p->next;
}
DNode q = L->next;
if(maxp = q){
return;
}
maxpre->next = maxp->next;
if(maxp->next != NULL){
maxp->next->prior = maxpre;
}
maxp->prior = L;
L->next = maxp;
maxp->next = q;
q->prior = maxp;
}2.35. 设有一个带头结点的非循环双链表 L, 其每个结点除了有 prior、data 和 next 域外,还有一个访问频度域 freq, 其值均初始化为 0。L 中各个结点的值都不相同,每当在链表中执行一次 Locate(L, x)运算时,令值为 x 的结点中 freq 域的值增 1,并使此链表中的结点保持按访问频度递减的顺序排列,且最近访问的结点排在频度相同的结点之前,以便使频繁访问的结点总是靠近表头。试编写符合上述要求的 Locate(L, x)函数,返回找到结点的地址,类型为指针型。
c
DNode Locate(DLinkList L, int x){
if(L->next == NULL){
return NULL;
}
DNode *p = L->next,*pre = L;
while(p != NULL){
if(p->data == x){
break;
}
pre = p;
p = p->next;
}
if(p->prior->data = p->data || p->prior = L){
return p;
}
pre->next = p->next;
if(p->next != NULL){
p->next->prior = pre;
}
DNode q = L->next;
pre = L;
while(q->data > p->data){
pre = q;
q = q->next;
}
p->prior = pre;
pre->next = p;
p->next = q;
q->prior = p;
return p;
}2.36. 有一个不带头结点的单链表 L, L 中各个结点的值都不相同,请设计一个递归算法,查找链表 L 中的最小值结点。
c
DNode *Find_Min(DNodeList L){
if(L == NULL || L->next == NULL){
return L;
}
DNode *p = Find_Min(L->next);
if(p->data > L){
return L;
}{
return p;
}
}2.37. 栈的结构体定义及基本操作。
c
#define MaxSize 50
typedef struct{
int data[MaxSize];
int top;
} Stack;
void InitStack(Stack &S){
S.top = -1;
}3. 栈和队列
3.1. 有一个带头结点的单链表 L, 结点结构由 data 和 next 两个域构成,其中 data 域为字符型。试设计一个算法判断该链表的全部 n 个字符是否中心对称。例如:xyx、yyx 都是中心对称。
c
int Func(LinkList L,int x){
char s[n/2];
LNode *p = L->next;
int i;
for(i = 0;i < n/2; i++){
s[i] = p->next;
}
if(n % 2 == 1){
p = p->next;
}
while( p != NULL){
if(p->data != s[i].data){
return 0;
}
p = p->next;
i--;
}
return 1;
}3.2. 假设一个算术表达式中包含小括号和中括号 2 种类型的括号,编写一个算法来判别表达式中的括号是否配对,假设算术表达式存放于字符数组中,以字符“\0”作为算术表达式的结束符。
c
int BracketCheck(char a[]){
Stack S;
InitStack(S);
char x;
for(int i,a[i] != '\n', i++){
switch(a[i]){
case '(':
Push(S, a[i]);
break;
case '[':
Push(S,a[i]);
break;
case ')':
if(IsEmpty(S)) return 0; // 每次出栈之前记得判空
Pop(S, x);
break;
case ']':
if(IsEmpty(S)) return 0;
Pop(S, x);
break;
default:
break;
}
}
if(IsEmpty(S)){
return 1;
}else{
return 0;
}
}3.3. 有两个栈 s1、s2 都采用顺序栈方式,并共享一个存储区 [0,...,maxsize-1], 为了尽量利用空间,减少溢出的可能,可采用栈顶相向、迎面增长的存储方式。试设计写出此栈的定义和 s1、s2 有关入栈和出栈的操作算法。
c
// 共享栈
#define MaxSize 50
typedef struct {
int data[MaxSize];
int top[2];
} Stack;
Stack s;
s.top[0] = -1;
s.top[1] = MaxSize;
int Push(int i, int x){
if(i > 1 || i < 0){
return 0;
}
if(s.top[1] - s.top[0] == 1){
return 0;
}
switch(i){
case 0:
s.top[0]++;
s.data[s.top[0]] = x;
break;
case 1:
s.top[1]--;
s.data[s.top[1]] = x;
break;
}
return 1;
}
int Pop(int i, int x){
if(i > 1 || i < 0){
return 0;
}
switch(i){
case 0:
if(s.top[0] == -1){
return 0;
}else{
x = s.data[s.top[0]--];
}
break;
case 1:
if(s.top[1] == MaxSize){
return 0;
}else{
x = s.data[s.top[1]++];
}
}
return 1;
}3.4. 队列的结构体定义与基本操作
c
#define MaxSize 50
typedef struct{
int data[MaxSize];
int front,rear;
} Queue;
void InitQueue(Queue &Q){
if(Q.front == Q.rear){
return 1;
}
return 0;
}
int EnQueue(Queue &Q,int x){
if(Q.rear == MaxSize){
return 0;
}
Q.data[Q.rear] = x;
Q.rear++;
return 1;
}
int DeQueue(Queue &Q,int x){
if(Q.rear == Q.front){
return 0;
}
x = Q.data[Q.front];
Q.front++;
return 1;
}
// 循环队列
Q.front == Q.rear; // 判空
Q.front == (Q.rear+1) % MaxSize; // 判满
int EnQueue(Queue &Q,int x){
if((Q.rear + 1) % MaxSize == Q.front){
return 0;
}
Q.data[Q.rear] = x;
Q.rear = (Q.rear + 1) % MaxSize;
return 1;
}
int DeQueue(Queue &Q,int x){
if(Q.rear == Q.front){
return 0;
}
x = Q.data[Q.front];
Q.front = (Q.front+1) % MaxSize;
return 1;
}3.5. 若希望循环队列中的元素都能得到利用,则需设置一个标志域 tag, 并以 tag 的值为 0 或 1 来区分队头指针 front 和队尾指针 rear 相同时的队列状态是 "空" 还是 "满"。试编写与此结构相应的入队和出队算法。
c
// 仅需在结构体里多加一个tag位
// 当入队时判断tag,当tag == 1 && Q.rear == Q.front return 0; 结束入队tag = 1
// 当出队时判断tag,当tag == 0 && Q.rear == Q.front return 0; 结束出队tag = 03.6. Q 是一个队列,S 是一个空栈,实现将队列中的元素逆置的算法。
c
void Reverse(Queue &Q, Stack S){
int x;
while(!IsEmpty(Q)){
DeQueue(Q,x);
Push(S,x);
}
while(!Empty(S)){
Pop(S,x);
EnQueue(Q,x);
}
}4. 树
4.1. 利用递归求解 n 的阶乘
c
int Func(int n){
if(n == 0){
return 1;
}
return n * Func(n-1);
}4.2. 斐波那契数列是满足 F(0)= 1, F(1)= 1, F(n)= F(n-1)+F(n-2)(n≥2)的数列,数列的前几项为 1,1,2,3, 5,8,13,21,…。写出求解斐波那契数列第 n 项的程序。
c
int Func(int n){
if(n == 0 || n == 1){
return 1;
}
return Func(n-1) + Func(n-2);
}4.3. 二叉树的链式存储结构体定义
c
typedef struct BiTNode{
int data;
struct BitNode *lchild,*rchild;
} BiTNode, *BiTree;4.4. 请分别写出二叉树的先序, 中序和后序递归遍历算法。
c
// 以先序为例
void PreOrder(BiTree T){
if(T == NULL) return;
printf("%d", T->data);
PreOrder(T->lchild);
PreOrder(T->rchild);
}4.5. 在一棵以二叉链表为存储结构的二叉树中,查找 data 域值等于 key 的结点是否存在,如果存在,则将指针 q 指向该结点,假设 data 为 int 型。(二叉树中结点值都不相同)
c
void Search(BiTree T,BNode *&q,int key){
if(T == NULL) return;
if(T->data == key){
q = T;
}else{
Search(T->lchild, q, key);
Search(T->rchild, q, key);
}
}4.6. 假设二叉树采用二叉链表形式存储,设计一个算法,求先序遍历序列中第 k(1≤k≤ 二叉树中结点个数)个结点的值。
c
int n; // 定义成全局变量
void Search_k(BiTree T, int k){
if(T == NULL) return;
n++;
if(n == k){
printf("%d", T->data);
}
Search_k(T->lchild,k);
Search_k(T->rchild,k);
}4.7. 利用递归计算二叉树中所有结点的个数.
c
// 法一:
int n = 0;
void Count(BiTree T){
if(T == NULL) return;
n++;
Count(T->lchild);
Count(T->rchild);
}c
// 法二:
int Count(BiTree T){
if(T == NULL) return 0;
int n1 = Count(T->lchild); // 局部变量的使用 叶子结点返回 1
int n2 = Count(T->rchild);
return n1 + n2 + 1;
}4.8. 利用递归计算二叉树中所有叶子结点的个数.
c
// 法二
int Count(BiTree T){
int n1,n2;
if(T == NULL) return;
if(T->lchild == NULL && T->rchild == NULL){
return 1;
}else{
n1 = Count(T->lchild);
n2 = Count(T->rchild);
return n1 + n2;
}
}4.9. 利用递归计算二叉树中所有双分支结点个数
c
int Count(BiTree T){
int n1,n2;
if(T == NULL) return;
n1 = Count(T->lchild);
n2 = Count(T->rchild);
if(T->lchild && T->rchild){
return 1 + n1 + n2;
}else{
return n1 + n2;
}
}4.10. 利用递归计算二叉树中所有单分支结点个数
c
int Count(BiTree T){
int n1,n2;
if(T == NULL) return;
n1 = Count(T->lchild);
n2 = Count(T->rchild);
if(T->lchild && T->rchild){
return n1 + n2;
}else if(T->lchild || T->rchild){
return n1 + n2 + 1;
}else{
return 0;
}
}4.11. 求一颗二叉树的深度
c
int Depth(BiTree T){
int ldep,rdep;
if(T == NULL) return 0;
ldep = Depth(T->lchild);
rdep = Depth(T->rchild);
if(ldep > rdep){
return ldep + 1;
}else{
return rdep + 1;
}
}4.12. 设树 B 是一棵采用二叉链表形式存储的二叉树编写一个把树 B 中所有结点的左、右子树进行交换的函数。
c
void ChangeChild(BiTree &T){
BNode *p;
if(T == NULL) return;
p = T->lhild;
T->lchild = T->rchild;
T->rchild = p;
ChangeChild(T->lchild);
ChangeChild(T->rchild);
}4.13. 假设二叉树采用二叉链表存储结构,设计一个算法,求二叉树 T 中值为 x 的结点的层次号。
c
void Search_x_level(BiTree T,int x,int level){ // 此处的level = 1
if(T != NULL){
if(T->data == x){
printf("%d",level);
}
Search_x_level(T->lchild,x,level+1);
Search_x_level(T->rchild,x,level+1);
}
}4.14. 请写出二叉树层次遍历算法
c
// 非递归
void LevelOrder(BiTree T){
BiTNode p = T;
Queue Q; // 定义一个辅助队列
InitQueue(Q);
EnQueue(p);
while(!IsEmpty(Q)){
DeQueue(Q,p);
printf("%d",p->data);
if(p->lchild){
EnQueue(Q,p->lchild); // p的左孩子入队,下一次循环出队时p = p->*child
}
if(p->rchild){
EnQueue(Q,p->rchild);
}
}
}4.15. 试写出二叉树的自下而上、从右到左的层次遍历算法
c
void ReverseLevelOrder(BiTree T){
Queue Q;
Stack S;
InitQueue(Q);
InitStack(S);
BiTNode *p = T;
EnQueue(Q, p);
while(!IsEmpty(Q)){
DeQueue(Q,p);
Push(S, p); // 不打印,而是压栈
if(p->lchild){
EnQueue(Q,p->lchild); // p的左孩子入队,下一次循环出队时p = p->*child
}
if(p->rchild){
EnQueue(Q,p->rchild);
}
}
while(!IsEmpty2(S)){
Pop(S,p);
printf("%d",p->data);
}
}4.16. 二叉树按二叉链表形式存储,写一个判别给定二叉树是否是完全二叉树的算法
c
int IsComplete(BiTree T){
if(T == NULL) return 1;
Queue Q;
InitQueue(Q);
BiTNode *p = T;
EnQueue(Q, p);
while(!IsEmpty(Q)){
DeQueue(Q, p);
if(p != NULL){
EnQueue(Q, p->lchild);
EnQueue(Q, p->rchild);
}else{
while(!IsEmpty(Q)){ // p为空,Q不为空的情况 |p(此时p为空)|NULL|NULL|NULL|
DeQueue(Q,p);
if(p != NULL){
return 0;
}
}
}
}
return 1;
}4.17. 已知二叉树采用二叉链表形式存储,设计一个算法完成:对于树中每个元素值为 x 的结点,删去以它为根的子树,并释放相应的空间。
c
void DeleteTree(BiTree &T){
if(T != NULL){
DeleteTree(T->lchild);
DeleteTree(T->rchild);
free(T);
}
}
void SearchX(BiTree &T, int x){
if(T == NULL) return;
Queue Q;
InitQueue(Q);
BiTNode *p;
while(!IsQueue(Q)){
DeQueue(Q, p);
if(p->lchild){
if(p->lchild->data == x){
DeleteTree(T->lchild);
T->lchild = NULL;
}else{
EnQueue(Q, p->lchild);
}
}
if(p->rchild){
if(p->rchild->data == x){
DeleteTree(T->rchild);
T->rchild = NULL;
}else{
EnQueue(Q, p->rchild);
}
}
}
}4.18. 非递归算法求二叉树高度.
c
``` int Depth(BiTree T){
if(T == NULL) return 0;
int h = 0, last = 0;
BiTNode *Q [MaxSize];
int front = -1, rear = -1;
BiTNode *p = T;
Q [++rear] = p;
while(! IsEmpty(Q)){
p = Q [++front];
if(p-> lchild){
Q [++rear] = p-> lchild;
}
if(p-> rchild){
Q [++rear] = p-> rchild;
}
if(front == last){
last = rear;
h++;
}
}
return h;
}4.19. 假设二叉树采用二叉链表存储结构,设计一个算法,求给定的二叉树宽度(即具有结点数最多的那一层的结点个数)。(有辣么一坨变量,啊啊啊)
c
int Width(BiTree T){
if(T == NULL) return;
BTNode *Q [MaxSize]; // 用于层序遍历
int front = 0, rear = 0;
int level [MaxSize]; // 用来存储结点属于哪一个层级
BiTree *p;
int k = 1; // 用于记录层级
Q [rear] = p;
level [rear] = k;
rear++;
while(front < rear){
p = Q [front];
k = level [front];
front++;
if(p-> lchild){
Q [rear] = p-> lchild;
level [rear] = k+1; // 层级+1
rear++;
}
if(p-> lchild){
Q [rear] = p-> rchild;
level [rear] = k+1;
rear++;
}
}
// while 循环结束, level 里存有这样的数据 |1|2|2|3| 对应 |第一层|第二层|第三层
int max = 0, n, i = 0; // i 是用于遍历 level 的
k = 1; // 重置 k
while(i < rear){
n = 0;
while(i < rear && level [i] == k){
n++; // n 会在每轮重置, 记录宽
i++; // i 是一直在+的
} // 一层结束
k++; // 层级+1
if(n > max){
max = n;
}
}
return max;
}4.20. 请写出中序非递归遍历二叉树的算法
c
void MidOrder(BiTree T){
Stack S;
InitStack(S);
BiTNode *p = T;
while(p || ! IsEmpty(S)){
if(p != NULL){
//print("%d", p); // 先序
Push(S, p);
p = p-> lchild;
}else{
Pop(S, p);
print("%d", p);
p = p-> rchild;
}
}
}4.21. 请写出后序非递归遍历二叉树的算法
起手:
int p, r; Stack S
c
// 需要定义一个指针 r, 指向结点的右结点
void PostOrder(BiTree T){
Stack S;
InitStack(S);
BiTNode *p = T;
BiTNode *r = NULL;
while(p || ! Empty(S)){ // [! code highlight]
if(p != NULL){ // [! code highlight]
Push(S, p); // [! code highlight]
p = p-> lchild; // [! code highlight]
}else{ // [! code highlight]
if(p-> rchild && p-> rchild != r){ // [! code highlight]
GetTop(S, p);
p = p-> rchild;
}else{
Pop(S, p); // [! code highlight]
printf("%d", p);
r = p; // [! code highlight]
p = NULL; // 易漏 // [! code highlight]
}
}
}
}4.22. 在二叉树中查找值为x的结点,试编写算法打印值为x的结点的所有祖先,假设值为x的结点不多于一个。
c
void Func(BiTree T, int x){
Stack S;
InitStack(S);
BiTNode *p = T,* r = NULL;
while(p || ! IsEmpty(S)){
if(p != NULL){
Push(S, p);
p = p-> lchild; // [! code highlight]
}else{
GetTop(S, p);
if(p-> rchild && p-> rchild != r){
p = p-> rchild; // [! code highlight]
}else{
Pop(S, p);
if(p-> data == x){
while(! IsEmpty(S)){
Pop(S, p);
printf("%d", p-> data)
}
}
r = p;
p = NULL;
}
}
}
}4.23. p和q分别为指向一棵二叉树中任意两个结点的指针,试编写算法找到p和q最近公共结点并返回
对后序遍历算法的改写
c
BiTree *FindAncestor(BiTree T, BiTNode p, BiTNode q){
BiTNode *bt = T,* r = NULL;
BiTNode * S [MaxSize], S1 [MaxSize], S2 [MaxSize];
int top = -1, top1 = -1, top2 = -1;
int temp;
while(p || top != -1){
if(bt != NULL){
S [++top] = bt; // [! code highlight]
bt = bt-> lchild;
}else{
bt = S [top];
if(bt-> rchild && bt-> rchild != r){
bt = bt-> rchild;
}else{
bt = S [top--]; // [! code highlight]
if(bt == p){
for(temp = 0; temp < top; temp++){
S1 [temp] = S [temp];
top1++;
}
}
if(bt == q){
for(temp = 0; temp < top; temp++){
S2 [temp] = S [temp];
top2++;
}
}
r = bt;
bt = NULL;
}
}
}
for(int i = top1; i >= 0; i--){
for(int j = top2; j >= 0; j--){
if(S1 [i] == S2 [j]){
return S1 [i];
}
}
}
return NULL;
}4.24. 假设一棵二叉树以二叉链表存储方式存储,请设计一个算法,输出根结点到每个叶子结点的路径。
c
void AllPath(BiTree T){
BiTNode *p = T, * r = NULL;
BiTNode *S [MaxSize];
int top = -1;
while(p != NULL || top == -1){
if(p != NULL){
S [++top] = p;
p = p-> lchild;
}else{
p = S [top--];
if(p-> lchild == NULL && p-> rchild == NULL){
for(int i = top, i >= 0, i--){
printf("%d", S [i]-> data);
}
print("%d", p-> data);
}
}
r = p;
p = NULL;
}
}4.25. 设计一个算法将二叉树的叶子结点按从左到右的顺序连成一个单链表,表头指针为head。二叉树按二叉链表方式存储,链接时用叶子结点的右指针域来存放单链表指针。
c
BiTNode *head = NULL, * pre = NULL;
void Link(BiTree &T){
if(T!= NULL){
Link(T-> lchild);
if(T-> lchild == NULL && T-> rchild == NULL){
if(pre == NULL){
head = T;
pre = T;
}else{
pre-> rchild = T;
pre = T
}
}
}
}4.26. 表达式(a-(b+c)*(d/e)存储在如下图所示的一棵以二叉链表为存储结构的二叉树中(二叉树结点的 data域为字符型),编写程序求出该表达式的值(表达式中的操作数都是一位的整数)。说明:函数 int op(int A,int B,char C)返回的是以C为运算符,以A、B为操作数的算式的数值,例如,若C为"+",则返回A+B的值。
c
int Compute(BiTree T){
if(T == NULL){
return 0;
}
int A, B;
if(T-> lchild == NULL && T-> rchild == NULL){
A = Compute(T-> lchild);
B = Compute(T-> rchild);
}else{
return T-> data - "0";
}
}4.27. 试设计判断两棵树是否相似的代码
c
int Similar(BiTree T1, BiTree T2){
int left, right;
if(T1 == NULL && T2 == NULL){
return 1;
}else if(T1 == NULL || T2 == NULL){
return 0;
}else{
left = Similar(T1-> lchild, T2-> lchild);
right = Similar(T1-> rchild, T2-> rchild);
return left && right;
}
}4.28. 在二叉树的二叉链表存储结构中,增加一个指向双亲结点的parent指针,设计一个算法,给这个指针赋值,并输出所有结点到根结点的路径。
c
typedef struct BiTNode{
char data;
struct BiTNode *left, * right, *parent;
} BiTNode, *BiTree;
void Func(BiTree &T, BiTNode *q){
if(T != NULL){
T-> parent = q;
q = T;
Func(T-> lchild);
Func(T-> rchild);
}
}
void PathPrint(BiTNode *p){
while(p != NULL){
printf("%c", p-> data);
p = p-> parent;
}
}
void AllPrint(BiTree T){
if(T != NULL){
pathPrint(T);
AllPrint(T-> lchild);
AllPrint(T-> rchild);
}
}4.29. 有一棵二叉树以顺序存储的方式存在一维数组A中,树中结点存储数据为字符型,空指针域在数组中以字符'#'表示,请设计一个算法将其改为二叉链表的存储方式。(假设数组A从下标1开始存储元素,存储元素个数为n)
c
BiTree Create(char A [], int i, int n){
if(i > n || A [i] == '#'){
return NULL;
}else{
BiTNode *p = (BiTNode *)malloc(sizeof(BiTree));
p-> data = A [i];
p-> lchild = Create(A, 2*i, n);
p-> rchild = Create(A, 2*i+1, n);
return p;
}
}4.30. 设一棵二叉树中各结点的值互不相同,其先序遍历序列和中序遍历序列分别存于两个一维数组 A[1...n]和B[1...n]中,试编写算法建立该二叉树的二叉链表。(这tm是什么东西,理解不能)
c
BiTree Create(char A [], int L1, int h1, char B [], int L2, int h2){
BiTNode *p = (BiTNode *)malloc(sizeof(BTNode));
p-> data = A [i];
int i;
for(i = L2; B [i] != p-> data, i++);
int llen = i-L2;
int rlen = h2-i;
if(llen) p-> lchild = Create(A, L1+1, L1+llen, B, L2+len-1, h1);
else p-> lchild = NULL;
if(rchild) p-> rchild = Create(A, h1-rlen+1, h1, B, h2-rlen+1, h2);
else p-> rchild = NULL;
return p;
}4.31. 设有一棵满二叉树(所有结点值均不同),已知其先序序列为pre,设计一个算法求其后序序列post
c
void PreToPost(char pre [], int l1, int h1, char post [], int l2, int h2){
int half;
if(h1 >= l1){
post [h2] = pre [l1];
half = (h1 - h2)/2;
PreToPost(pre, l1+1, l1+half, post, l2, l2+half-1);
PreToPost(pre, l1+1+half, h1, post, l2+half, h2-1);
}
}5. 查找和排序
5.1. 数组A[]中有个整数,没有次序,数组从下标1开始存储,请写出查找任一元素k的算法,若查找成功,则返回元素在数组中的位置;若查找不成功,则返回0。
c
略 一个 for 循环5.2. 已知一个顺序表L,其中的元素递增有序排列,请分别写出折半查找的递归算法和非递归算法查找L中值为key的元素位置。
c
int BinarySearch(SqList L, int key){
int low = 0, high = L.length - 1, mid;
while(low <= high){
mid = (low+high)/2;
if(L.daata [mid] == key){
return mid;
}else if(L.data [mid] > key){
high = mid -1;
}else{
low = mid + 1;
}
}
return -1;
}c
int BinarySearch(SqList L, int key, int low, int high){
if(low > high) return -1;
int mid = (low+high)/2;
if(L.data [mid] < key){
return BinarySearch(L, key, mid+1, high);
}else if(L.data [mid] > key){
return BinarySearch(L, key, low, mid-1);
}else{
return mid;
}
}5.3. 线性表中各结点的检索概率不等时,可用如下策略提高顺序检索的效率:若找到指定的结点,则将该结点和其前驱结点(若存在)交换,使得经常被检索的结点尽量位于表的前端。试设计在顺序结构和链式结构的线性表上实现上述策略的顺序检索算法。
c
void SqListSearch(SqList &L, int k){
if(L.data [0] == k){
return;
}
for(int i = 1; L.length-1; i++){
if(L.data [i] == k){
int temp;
temp = L.data [i];
L.data [i] = L.data [i-1];
L.data [i-1] = temp;
}
}
}c
void LinkListSearch(LinkList &L, int k){
if(p-> next-> next-> data == k){
return;
}
LNode *p = L;
while(p-> next-> next){
if(p-> next-> next-> data = k){
LNode *q = p-> next, * r = p-> next-> next;
q-> next = r-> next;
p-> next = r;
r-> next = q;
return;
}
p = p-> next;
}
}5.4. 请分别写出在二叉排序树中查找数据域值为k结点位置的递归算法和非递归算法。
c
BiTNode *Search(BiTree T, int k){
while(T!= NULL){
if(T-> data > k){
T = T-> lchild;
}else if(T-> data < k){
T = T-> rchild;
}else{
return T;
}
}
return NULL;
}c
BiTNode *Search(BiTree T, int k){
if(T == NULL){
return NULL;
}else {
if(T-> data == k){
return T;
}else if(T-> data > k){
return Search(T-> lchild, k);
}else {
return Search(T-> rchild, k);
}
}
}5.5. 请写出在一棵二叉排序树T中插入值为k结点的算法,插入成功则返回1,插入失败则返回0,然后写出根据数组A中存储元素值顺序构造一棵二叉排序树的算法,假设数组A的长度为。
c
// 插入
int BST_Insert(BiTree &T, int k){
if(T == NULL){
T = (BiTNode *)malloc(sizeof(BiTNode));
T-> data = k;
T-> lchild = NULL;
T-> rchild = NULL;
return 1;
}else if(T-> data > k){
return BST_Insert(T-> lchild, k);
}else if(T-> data < k){
return BST_Insert(T-> rchild, k);
}else {
return 0;
}
}
// 构造
void Create_BST(BiTree &T int A [], int n){
T = NULL;
int i = 0;
while(i < n){
BST_Insert(T, A [i]);
i++;
}
}5.6. 设计一个算法,求出给定二叉排序树中最小和最大的关键字
c
略 一个 while 循环5.7. 试编写一个算法,求出指定结点在给定二叉排序树中的层次。
c
int level(BiTree T, BiTNode *p){
int n = 1;
while(T != p){
if(T-> data < p-> data){
T = T-> rchild;
}else{
T = T-> lchild;
}
n++;
}
return n;
}5.8. 设计一个算法,从大到小输出二叉排序树中所有值不小于k的关键字
c
void Func(BiTree T, int k){
if(T != NULL){
Func(T-> rchild, k);
if(T-> data >= k){
printf("%d", T-> data);
}
Func(T-> lchild, k);
}
}5.9. 试编写一个算法,判断给定的二叉树是否是二叉排序树。
c
// 改写中序遍历
int JudgeBST(BiTree T, int &pre){
int b1, b2;
if(T == NULL){
return 1;
}else{
b1 = JudgeBST(T-> lchild, pre);
if(b1 == NULL || T-> data <= pre){
return 0;
}
pre = T-> data;
b2 = JudgeBST(T-> rchild, pre);
return b2;
}
}5.10. 试编写一个判断二叉排序树是否是平衡二叉树的算法。
c
int Func(BiTree T){
if(T == NULL){
return 0;
}
int left = Func(T-> lchild);
int right = Func(T-> rchild);
if(left == -1 || right == -1 || abs(left-right) > 1){
return -1;
}else{
return max(left, right) + 1; // 返回高度
}
}5.11. 在平衡二叉树的每个结点中增设一个域lsize,存储以该结点为根的左子树中的结点个数加一。编写一个算法,确定树中第k小结点的位置。
c
BTNode *Search_k(BiTree T, int k){
if(T == NULL || k < 1){
return NULL;
}else if(T-> lsize == k){
return T;
}else if(T-> lsize > k){
return Search_k(T-> child, k);
}else{
return Search_k(T-> rchild, k-T-> lchild);
}
}5.12. 编写一个递归算法,在一棵有n个结点的、随机建立起来的二叉排序树上查找第k小的元素,并返回指向该结点的指针。要求算法的平均时间复杂度为O(log_n)。二叉排序树的每个结点中除 data,lchild,.rchild等数据成员外,增加一个count成员,保存以该结点为根的子树的结点个数。
c
BiTNode *Search_k(BiTree T, int k){
if(k < 1 || k > T-> count){
return NULL;
}
if(T-> lchild == NULL){
if(k == 1){
return T;
}else{
return Search_k(T-> rchild, k-1);
}
}else{
if(T-> lchild-> count == k-1){
return T;
}else if(T-> lchild-> count > k-1){
return Search_k(T-> lchild, k);
}else{
return Search_k(T-> rchild, k-1-T-> lchild-> count);
}
}
}5.13. 请分别写出顺序存储和链式存储的直接插入排序算法
c
void InsertSort(int A [], int n){
int i, j;
for(i = 2; i <= n; i++){
if(A [i] < A [i-1]){
A [0] = A [i];
for(j = i-1; A [j] > A [0], j--){
A [j+1] = A [j];
}
A [j+1] = A [0];
}
}
}c
void InsertSort(SqList &L){
if(L-> next == NULL){
return;
}
LNode *pre,* q, *p,* r;
p = L-> next-> next;
L-> next-> next = NULL;
while(p != NULL){
pre = L;
q = pre-> next;
while(q != NULL && q-> data <= p-> data){
pre = q;
q = pre-> next;
}
r = p-> next;
p-> next = q;
pre-> next = p;
p = r;
}
}5.14. 有一个数组A存储着m+n个整型元素,元素从下标1开始存储,其前m个元素递增有序,后n个元素递增有序,请设计一个算法使这个数组整体有序。
c
void InsertSort(int A [], int m, int n){
int i, j;
for(i = m+1; i < m+n; i++){
if(A [i] < A [i-1]){
A [0] = A [i];
for(j = i-1; A [j] < A [0]; j--){
A [j+1] = A [j];
}
A [j+1] = A [0];
}
}
}5.15. 请写出折半插入排序算法。
c
void InsertSort(int A [], int n){
int i, j, low, high, mid;
for(i = 2; i <= n; i++){
A [0] = A [i];
low = 1;
high = i - 1;
while(low <= high){
mid = (low+high)/2;
if(A [mid] > A [0]){
high = mid - 1;
}else {
low = high + 1;
}
}
for(j = i-1; j >= low; j--){
A [j+1] = A [j];
}
A [j+1] = A [0];
}
}5.16. 请写出冒泡排序的算法
c
void BubbleSort(int A [], int n){
int i, j, temp;
int flag;
for(i = 0; i < n-1; i++){
flag = 0;
for(j = n-1; j > i; j--){
if(A [j-1] > A [j]){
temp = A [j];
A [j] = A [j-1];
A [j-1] = temp;
flag = 1;
}
}
if(flag == 0){
return;
}
}
}5.17. 编写双向冒泡排序算法,在正反两个方向交替进行扫描,即第一趟把关键字最大的元素放在序列的最后面,第二趟把关键字最小的元素放在序列的最前面,如此反复进行。
c
void Bubble(int A [], int n){
int low = 0, high = n-1;
int temp, flag = 1;
while(low < high && flag == 1){
flag = 0;
for(i = low; i < high; i++){
if(A [i] > A [i+1]){
temp = A [i];
A [i] = A [i+1];
A [i+1] = A [i];
flag = 1;
}
}
high--;
for(i = high; i > low; i--){
if(A [i] < A [i-1]){
temp = A [i];
A [i] = A [i-1];
A [i-1] = A [i];
flag = 1;
}
}
low--;
}
}5.18. 请写出快速排序算法
c
// 单次划分
int Partition(int A [], int low, int high){
int pivot = A [low];
while(low < high){
while(low < high && A[high] > = pivot){
high--;
}
A [low] = A [high];
while(low < high && A [low] <= pivot){
low++;
}
A [high] = A [low];
}
A [low] = pivot;
return low;
}
// 快速排序
void QuickSort(int A [], int low, int high){
if(low < high){
int pivotpos = Partition(A, low, high);
QuickSort(A, low, pivotpos-1);
QuickSort(A, pivotpos+1, high);
}
}5.19. 有一个整型数组A存储了n个元素,其元素序列是无序的,元素从下标为1开始存储,请设计一个算法让数组A中的最后一个元素放在数组A整体排序后的正确位置上,结果返回其数组下标,要求关键字的比较次数不超过n。
c
int Partition(int A [], int n){
int low = 0, high = n;
int pivot = A [high];
while(low < high){
while(low < high && A[high] > = pivot){
high--;
}
A [low] = A [high];
while(low < high && A [low] <= pivot){
low++;
}
A [high] = A [low];
}
A [low] = pivot;
return low;
}5.20. 请设计一个尽可能高效的算法,使之能够在数组A[1..]中找出第k小的元素(即从小到大排序后处于第k个位置的元素)。
c
int Search_k(int A [], int low, int high, int k){
int pivot = A [low];
int low_temp = low, high_temp = high;
while(low < high){
while(low < high && A[high] > = pivot){
high--;
}
A [low] = A [high];
while(low < high && A [low] <= pivot){
low++;
}
A [high] = A [low];
}
A [low] = pivot;
if(low == k){
return low;
}else if( low > k){
return Search_k(A, low_temp, low-1, k);
}else{
return Search_k(A, low+1, high_temp, k);
}
}5.21. 已知一个数组A存储了n个元素,且数组中每个元素都是不相同的正整数,请设计一个高效算法把数组A中所有奇数移动到所有偶数前边的算法。
c
void Move(int A [], int n){
int low = 0, high = n-1, temp;
while(low < high){
while(low < high && A [low] % 2 != 0){
low++;
}
while(low < high && A [low] % 2 != 1){
high--;
}
if(low < high){
temp = A [low];
A [low] = A [high];
A [high] = A [low];
low++;
high--;
}
}
}5.22. 顺序放置n个球,每个球的颜色是红,白,蓝之一,要求重新排列这些球,使得所有红色的球在前白色球居中,蓝色的球在后。假设放置球的序列存放在数组A中,0代表球为红色,1代表球为白色 2代表球为蓝色,请设计一个算法为这个球排序。
c
void Sort(int A [], int n){
int low = 0, high = n-1, i = 0;
while(i <= high){
if(A [i] == 0){
Swap(A [i], A [low]);
low++;
i++;
}else if(A [i] == 1){
i++;
}else{
Swap(A [i], A [high]);
high--;
}
}
}5.23. 简单选择排序
c
void SelectSort(int A []){
int i, j, min, temp;
for(i = 0, i < n-1; i++){
min = i;
for(j = i+1; i < n; j++){
if(A [i] < A [min]){
min = j;
}
}
temp = A [i];
A [i] = A [min];
A [min] = temp;
}
}c
void SelectSort(LinkList &L){
LNode *pre, * p, *maxpre, * maxp;
LNode *r = L; // 记录已排好序的最后一个结点
while(r-> next != NULL){
pre = r;
p = r-> next;
maxpre = pre;
max = p;
// 找 maxp
while(p != NULL){
if(p-> data > maxp-> data){
maxpre = pre;
maxp = p;
}
pre = p;
p = pre-> next;
}
// 开始交换(取下结点)
maxpre-> next = maxp-> next;
// 头插入结点
maxp-> next = L-> next;
L-> next == maxp;
if(r == L){
r = maxp;
}
}
}5.24. 有一种简单的排序算法称为计数排序,其算法思想是选取一个待排序的元素值,然后遍历整个数组,统计数组中有多少个元素比选取的待排序元素值小,假设统计出的计数值为C,则可以根据计数值c在新的有序数组中找到待排序元素的最终位置。现有一个数组A,存放了n个互不相同的整型元素,请使用计数排序算法为数组A排序,排序结果存放在数组B中。
c
void Count(int A [], int B [], int n){
int i, j;
int count;
for(i = 0; i < n; i++){
for(j = 0, count = 0; j < n; j++){
if(A [j] < A [i]){
count++;
}
}
B [count] = A [i];
}
}5.25. 有一个数组A存储了个整型元素,元素从数组下标1开始存储,请写出对数组A使用堆排序的算法
c
void HeapAdjust(int A [], int n, int k){
A [0] = A [k];
int i = 2*k;
while(i <= n){
if(i < n && A[i+1] > A [i]){
i++;
}
if(A [i] > A [0]){
A [k] = A [i];
k = i;
i = 2*i;
}else{
break;
}
}
A [k] = A [0];
}
void BuildMaxHeap(int A [], int n){
for(int i = n/2; i > 0; i--){
HeapAdjust(A, n, i);
}
}
void HeapSort(int A [], int n){
BuildMaxHeap(A, n);
int temp;
for(int i = n; i > 1; i--){
temp = A [1];
A [1] = A [i];
A [i] = temp;
HeapAdjust(A, i-1,1);
}
}5.26. 试设计一个算法,判断一个数据序列是否构成一个小根堆。
c
bool IsMinHeap(int A [],int len){
if(len%2 == 0){ //len 为偶数,有一个单分支结点
if(A [len/2] > A [len]) //判断单分支结点
return false;
for(i = len/2-1; i >= 1; i--) //判断所有双分支结点
if(A [i] > A [2 *i] || A[i]> A[2* i+1])
return false;
else{ //len 为奇数时,没有单分支结点
for(i = len/2; i >= 1; i--) //判断所有双分支结点
if(A [i] > A [2 *i] || A[i]> A[2* i+1])
return false;
}
return true;
}二路归并排序
c
void Merge(int sort [], int num [], int low, int mid, int high){
int i = low; //左子序列起点下标
int j = mid+1; //右子序列起点下标
int k = low; //临时数组的初始化下标
while(i <= mid&&j <= high){//在左右子序列中按从小到大顺序存到临时数组中
if(num [i] < num [j])
sort [k++] = num [i++];
else
sort [k++] = num [j++];
}
//将左右子序列剩余的数依次存入临时数组
while(i <= mid)
sort [k++] = num [i++];
while(j <= high)
sort [k++] = num [j++];
//将临时数组的数据按位置复制到原数组对应位置上
while(--k >= 0)
num [k] = sort [k];
}
void MergeSort(int sort [], int num [], int low, int high){
if(low < high){
int mid =(low+high)/2; //分为左右子序列的中间下标
MergeSort(sort, num, low, mid); //递归左子序列
MergeSort(sort, num, mid+1, high); //递归右子序列
Merge(sort, num, low, mid, high); //排序
}
}6. 图
6.1. 图的邻接矩阵存储结构定义及其基本操作
c
typedef struct MGraph{
char Vex [MaxSize];
int Edge [MaxSize][MaxSize];
int vexnum, arcnum;
} MGraph;6.2. 图的邻接表存储结构定义及其基本操作。
c
typedef struct ArcNode{
int adjvex;
struct ArcNode *nextarc;
} ArcNode;
typedef struct VNode{
char data;
ArcNode *firstarc;
} VNode;
typedef struct AGraph{
VNode adjlist [MaxSize];
int vexnum, arcnum;
} AGraph;6.3. 写出从图的邻接表表示转换成邻接矩阵表示的算法
c
void Func(MGraph &G1, AGraph *G2){
G1.vexnum = G2-> vexnum; // 复制值
G1.arcnum = G2-> arcnum;
for(int i = 0; i < G2-> vexnum; i++){
for(int j = 0; j < G2-> vexnum; j++){
G1 [i][j] = 0; // 初始化
}
}
ArcNode *p;
for(int i = 0; i < G2-> vexnum; i++){
G1.Vex [i] = G2-> adjlist [i].data;
p = G2-> adjlist [i].firstarc;
while(p != NULL){
G1.Edge [i][p->adjvex] = 1;
p = p-> nextarc;
}
}
}6.4. 写出从图的邻接矩阵表示转换成邻接表表示的算法。
c
void Func(MGraph G1; AGraph *G2){
G2-> vexnum = G1.vexnum;
G2-> arcnum = G1.vexnum;
for(int i = 0; i < G1.vexnum; i++){ // 给邻接表的 adjvex [] 赋值
G2-> adjlist [i].data = G1.Vex [i];
G2-> adjlist [i].firstarc = NULL;
}
ArcNode *p;
for(int i = 0; i < G1.vexnum; i++){
for(int j = 0; j < G1.vexnum; j++){
if(G1.Edge [i][j] != 0){
p = (ArcNode *)malloc(sizeof(ArcNode));
p-> adjvex = j; // 创建结点 ArcNode
p-> nextarc = G2-> adjlist [i].firstarc; // 对邻接表的结点数组进行头插操作
G2-> adjlist [i].firstarc = p;
}
}
}
}6.5. 请写出以邻接矩阵方式存储图的广度优先遍历算法
c
void BFS(MGraph G, int v, int visited []){
Queue Q;
InitQueue(Q);
printf("%c", G.Vex [v]);
visited [v] = 1;
EnQueue(Q, v);
-----------------------------
while(! IsEmpty(Q)){ // 逐层遍历
DeQueue(Q, v);
for(int j = 0; j < G.vexnum; j++){ // 一次广度遍历
if(G.Edge [v][j] == 1 && visited [i] == 0){
printf("%c", G.Vex [i]); // 打印 置 1 入队
visited [j] = 1;
EnQueue(Q, j);
}
}
}
}6.6. 请写出以邻接表方式存储图的广度优先遍历算法
c
void BFS(AGraph *G, int v, int visited []){
Queue Q;
InitQueue(Q);
print("%c", G-> adjlist [v].data);
visited [v] = 1;
EnQueue(Q, v);
ArcNode *p; // [! code highlight]
while(! IsEmpty(Q)){
DeQueue(Q, v);
p = G-> adjlist [v].firstarc;
while(p != NULL){ // [! code highlight]
if(visited [p-> adjvex] == 0){
printf("%c", G-> adjlist [p-> adjvex].data);
visited [p-> adjvex] = 1;
EnQueue(Q, p-> adjvex);
}
}
}
}6.7. 设计一个算法,找出邻接表方式存储的无向连通图G中距离顶点V最远的一个顶点。(所谓最远就是到达v的路径长度最长)
c
int Func(AGraph *G, int v, int visited []){
for(int i = 0; i < G-> vexnum; i++){
visited [i] = 0;
}
Queue Q;
InitQueue(Q);
visited [v] = 1;
EnQueue(Q, v);
ArcNode *p;
while(! IsEmpty(Q)){
DeQueue(Q, v); // 最后一个出队的 v 即所求
p = G-> adjlist [v].firstarc;
while(p != NULL){
if(visited [p-> adjvex] == 0){
visited [p-> adjvex] = 1;
EnQueue(Q, p-> adjvex);
}
p = p-> nextarc;
}
}
return v;
}6.8. 请写出利用BFS算法求解邻接表存储的图中单源最短路径的算法,
c
void BFS_MIN_Distance(AGraph *G, int v, int visited [], int d []){ // d [] 记录距离
for(int i = 0; i < G-> vexnum; i++){
visited [i] = 0;
d [i] = INT_MAX;
}
Queue Q;
InitQueue(Q);
ArcNode *p;
visited [v] = 1;
d [v] = 0;
EnQueue(Q, v);
while(! IsEmpty(Q)){
DeQueue(Q, v);
p = G-> adjlist [v].firstarc;
while(p != NULL){
if(visited [p-> adjvex] == 0){
visited [p-> adjvex] = 1;
d [p-> adjvex] = d [v]+1; // 源顶点的距离+1
EnQueue(Q, v);
}
p = p-> nextarc;
}
}
}6.9. 请写出以邻接矩阵方式存储图的深度优先遍历算法。
c
void DFS(MGraph G, int v, int visited []){
printf("%c", G.Vex [v]);
visited [v] = 1;
for(int j; j < G.vexnum; j++){
if(G.Edge [v][j] == 1 && visited [j] == 0){
DFS(G, j, visited); // for + if + 递归
}
}
}
void Func(MGraph G, int v){
int visited [G.vexnum];
for(int i = 0; i < G.vexnum; i++){
visited [i] = 0;
}
DFS(G, v, visited);
for(int i = 0; i < G.vexnum; i++){
if(visited [i] == 0){
DFS(G, i, visited);
}
}
}6.10. 请写出以邻接表方式存储图的深度优先遍历算法
c
void DFS(AGraph *G, int v, int visited []){
printf("%c", G-> adjlist.data);
visited [v] = 1;
ArcNode *p;
while(p != NULL){
if(visited [p-> adjvex] == 0){
DFS(G, p-> adjvex, visited);
}
}
}
void Func(AGraph *G, int v){
int visited [G-> vexnum];
for(int i = 0; i < G-> vexnum; i++){
visited [i] = 0;
}
DFS(G, v, visited);
for(int i = 0; i < G-> vexnum; i++){
if(visited [i] == 0){
DFS(G, i, visited);
}
}
}6.11. 有向图G以邻接表方式存储,请设计一个算法判断图G中顶点到顶点是否存在路径。i和j不相等
c
void DFS(AGraph *G, int v, int visited []){
printf("%c", G-> adjlist.data);
visited [v] = 1;
ArcNode *p;
while(p != NULL){
if(visited [p-> adjvex] == 0){
DFS(G, p-> adjvex, visited);
}
}
}
int Path_i_j(AGraph *G, int i, int j){
int visited [G-> vexnum];
for(int i = 0; i < G-> vexnum; i++){
visited [k] = 0;
}
DFS(G, i, visited);
if(visited [j] == 1){
return 1;
}else{
return 0;
}
}6.12. 请设计一个算法判断一个邻接表存储的无向图中有几个连通分量。
c
void DFS(AGraph *G, int v, int visited []){
printf("%c", G-> adjlist.data);
visited [v] = 1;
ArcNode *p;
while(p != NULL){
if(visited [p-> adjvex] == 0){
DFS(G, p-> adjvex, visited);
}
}
}
int Func(AGraph *G){
int visited [];
for(int i = 0; i < G-> vexnum; i++){
visited [i] = 0;
}
int count = 0;
for(int i = 0; i < G-> vexnum; i++){
if(visited [i] == 0){
DFS(G, i, visited); // [! code highlight]
count++; // [! code highlight]
}
}
return count;
}6.13. 试设计一个算法,判断一个邻接表存储的无向图G是否为一棵树,
c
void DFS(AGraph *G, int v, int visited []){
printf("%c", G-> adjlist.data);
visited [v] = 1;
ArcNode *p;
while(p != NULL){
if(visited [p-> adjvex] == 0){
DFS(G, p-> adjvex, visited);
}
}
}
int IsTree(AGraph *G){
int visited [G-> vexnum];
for(int i = 0; i < G-> vexnum; i++){
visited [i] = 0;
}
DFS(G, 0, visited);
for(int i = 0; i < G-> vexnum; i++){
if(visited [i] == 0){
return 0;
}
}
if(G-> arcnum == G-> vexnum-1){
return 1;
}else{
return 0;
}
}6.14. 有一个邻接矩阵形式存储的连通图G,试写出图G深度优先遍历的非递归算法。
c
void DFS(MGraph G, int v, int visited []){
for(int i = 0; i < G.vexnum; i++){
visited [i] = 0;
}
Stack S;
InitStack(S);
printf("%c", G.Vex [v]);
visited [v] = 1;
Push(S, v);
int j;
while(! IsEmpty(S)){
GetTop(S, v);
for(j = 0; j < G.vexnum; j++){
if(G.Edge [v][j] == 1 && visited [j] == 0){
break;
}
}
if(j == S.vexnum){
Pop(S, v);
}else{
printf("%c", G.Vex [j]);
visited [j] = 1;
Push(S, j);
}
}
}有一个邻接表形式存储的连通图G,试写出图G深度优先遍历的非递归算法
c
void DFS(AGraph *G, int v, int visited []){
for(int i = 0; i < G-> vexnum; i++){
visited [i] = 0;
}
Stack S;
InitStack(S);
printf("%c", G-> adjlist [v].data);
visited [v] = 1;
Push(S, v);
ArcNode *p;
while(! IsEmpty(S)){
GetTop(S, v);
p = G-> adjlist [v].firstarc;
while(p != NULL && visited [p-> adjvex] == 1){
p = p-> nextarc;
}
if(p == NULL){
Pop(S, v);
}else{
printf("%c", G-> adjlist [p-> adjvex].data);
visited [p-> adjvex] = 1;
Push(S, p-> adjvex);
}
}
}假设图用邻接表表示,设计一个算法,输出从顶点u到顶点的所有简单路径
c
void PrintPath(AGraph *G, int u, int v, int visited [], int path [], int d){
d++;
path [d] = G-> adjlist [u].data;
visited [u] = 1;
if(u == v){
for(int i = 0; i <= d; i++){
printf("%c", path [i]);
}
visited [u] = 0;
return;
}
ArcNode *p = G-> adjlist [u].firstarc;
while(p!= NULL){
if(visited [p-> adjvex] == 0){
PrintPath(G, p-> adjvex, v, visited, path, d);
}
p = p-> nextarc;
}
visited [u] = 0;
}请写出邻接表存储图的拓扑排序算法
c
typedef struct VNode{
char data;
int indegree;
ArcNode *firstarc;
}
int Top(AGraph G){
int i = 0, count = 0;
ArcNode *p;
Stack S;
InitStack(S);
// 找到初始入度为 0 的顶点
for(; i < G-> vexnum; i++){
if(G-> adjlist [i].indegree == 0){
Push(S, i);
}
}
// 进行拓补排序
while(! IsEmpty(S)){
Pop(S, i);
printf("%c", G-> adjlist [i].data);
count++;
p = G-> adjlist [i].firstarc;
// 对边表结点
while(p != NULL){
G-> adjlist [p-> adjvex].indegree--;
if(G-> arclist [p-> adjvex].indegree == 0){
Push(S, p-> adjvex);
}
p = p-> nextarc;
}
}
// 检查是否有环
if(count == G-> vexnum){
return 1;
}else{
return 0;
}
}请设计一个算法判断一个邻接表存储的无向图中是否有环。
c
// 判断有几个连通分量
int Func(AGraph *G){
int visited [];
for(int i = 0; i < G-> vexnum; i++){
visited [i] = 0;
}
int count = 0;
for(int i = 0; i < G-> vexnum; i++){
if(visited [i] == 0){
DFS(G, i, visited); // [! code highlight]
count++; // [! code highlight]
}
}
return count;
}
int Isloop(AGraph *G){
int n = Func(G);
if(G-> arcnum == G-> vexnum - 1){
return 1;
}else{
return 0;
}
}请写出构造最小生成树的Prim算法
两个数组,一个记录最小距离,用lowcost[j] = G.Edge[k][j];更新,一个用于标记是否visited
c
void Prim(MGraph G, int v){
int visited [G.vexnum];
int lowcost [G.vexnum];
// 初始化两个数组
for(int i = 0; i < G.vexnum; i++){
visited = 0;
lowcost = G.Edge [v][i];
}
printf("%d", G.Vex [v]);
visited [v] = 1;
int min, k;
for(int i = 0; i < G.vexnum - 1; i++){
min = INT_MAX;
// 找到距离最小的结点
for(int j = 0; j < G.vexnum; j++){
if(visited [j] == 0 && lowcost [j] < min){
min = lowcost [j];
k = j;
}
}
printf("%d", G.Vex [k]);
visited [k] = 1;
// 数组更新
for(int j = 0; j < G.vexnum; j++){
if(visited [j] == 0 && G.Edge [k][j] < lowcost [j]){
lowcost [j] = G.Edge [k][j];
}
}
}
}请写出构造最小生成树的Kruskal算法(两页多,写个钩子哦)
c
啊哈哈哈哈哈哈哈哈哈哈哈 ~~~~ ╰(‵□′)╯请写出求单源最短路径的Dijkstra算法
c
void Dijkstra(MGraph G, int v){
int visited [G.vexnum];
int dist [G.vexnum]; // 记录单元最短路径
int path [G.vexnum]; // 记录入度的结点
for(int i = 0; i < G.vexnum; i++){
visited [i] = 0;
}
for(int i = 0; i < G.vexnum; i++){
dist [i] = G.Edge [v][i];
path [i] = v;
}
visited [v] = 1;
int min, k;
for(int i = 0; i < G.vexnum; i++){
min = INT_MAX;
for(int j = 0; j < G.vexnum; j++){
if(visited [j] == 0 && dist [j] < min){
min = dist [j];
k = j;
}
}
visited [k] = 1;
for(int j = 0; j < G.vexnum; j++){
if(visited [j] == 0 && dist [k] + G.Edge [k][j] < dist [j]){
dist [j] = dist [k] + G.Edge [k][j];
path [j] = k;
}
}
}
}Floyd算法
c
什么玩意啊408真题
2015年:
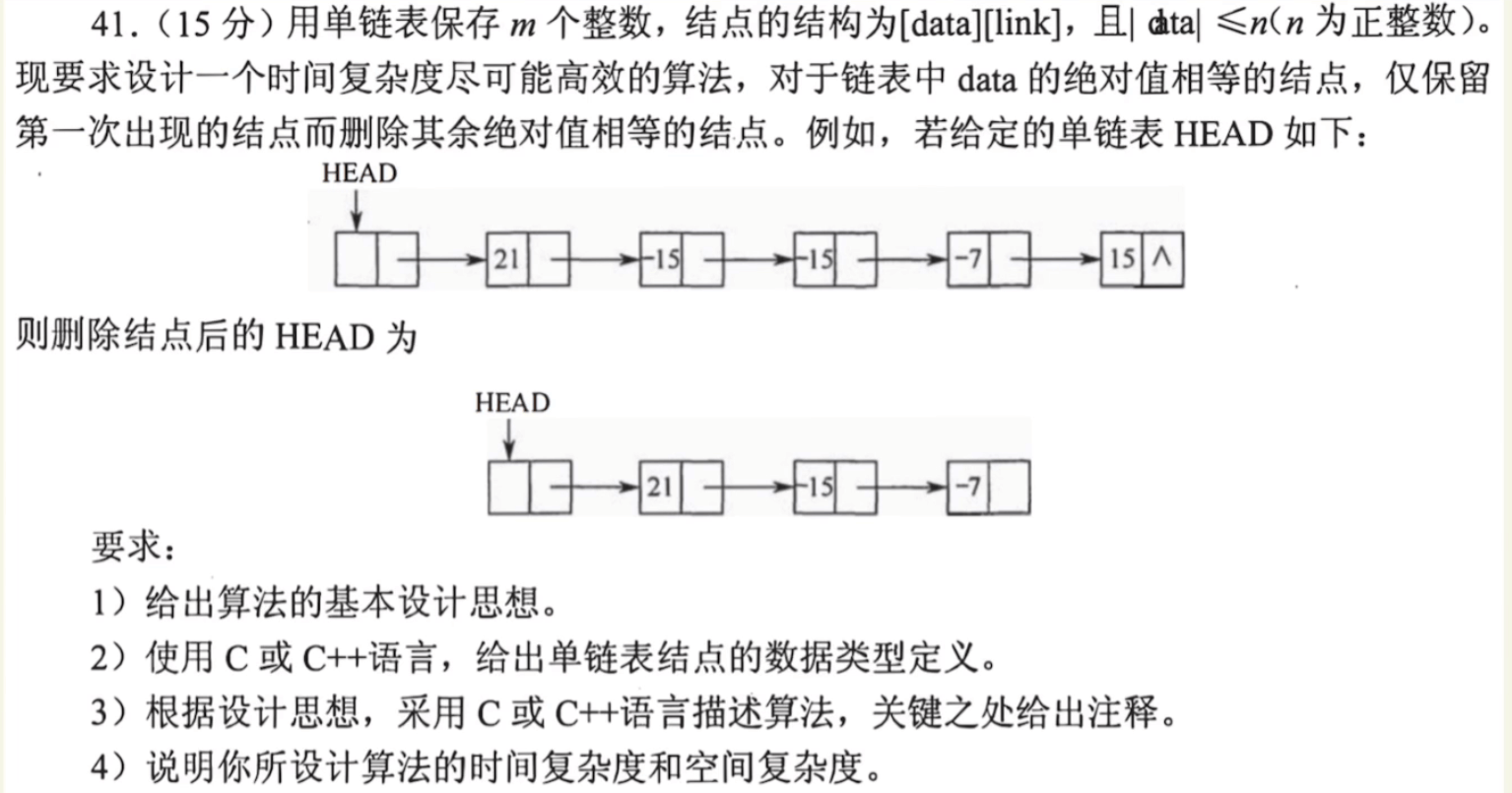
c
void Func(LinkList &HEAD, int n){
int *A = (int *)malloc(sizeof(int) * (n+1));
for(int i = 0; i < n+1; i++){
A [i] = 0;
}
int *pre = HEAD, p = HEAD-> link;
int m; // 用于接收绝对值
while(p != NULL){
m = p-> data > 0 ? p-> data : -(p-> data);
if(A [p-> data] == 0){
A [p-> data] = 1;
pre = p;
p = p-> link;
}else{
pre-> link = p-> link;
free(p);
p = pre-> link;
}
}
free(A);
}2016年:

c
// T: O(n) S: O(1)
int Func(int A [], int n){
int low = 0, high = n-1, k = n/2 - 1, flag = 1, low_twmp = 0, high_temp = n-1;
int S1 = 0, S2 = 0, pivot;
while(flag){
pivot = A [low];
while(low < high){
while(low < high && A[high] > pivot){
high--;
}
A [low] = A [high];
while(low < high && A [low] < pivot){
low++;
}
A [high] = A [low];
}
if(low == k){
flag = 0;
}else if(low > k){
high--;
high_temp = high;
low = low_temp;
}else{
low++;
low_temp = low;
high = high_temp;
}
}
for(int i = 0; i < k+1; i++){
S1 = S1+A [i];
}
for(int i = k+1, i < n; i++){
S2 = S2+A [i];
}
return S2-S1;
}2017年:
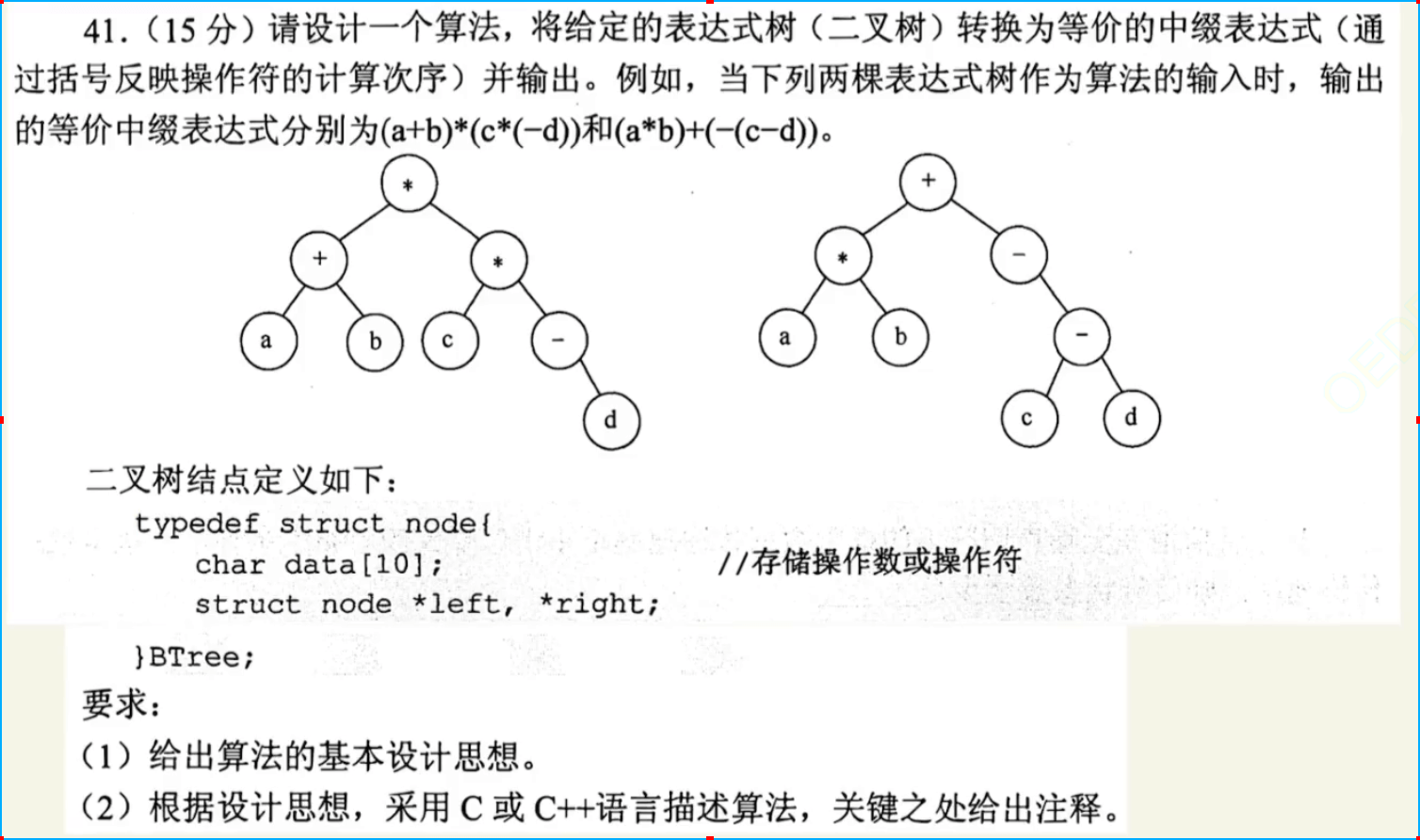
c
void Func(BTree *T, int deep){ // 初始传入 1
if(T != NULL){
if(T-> lchild == NULL && T-> rchild == NULL){
printf("%s", T);
}else{
if(deep > 1){
printf("(");
}
Func(T-> lchild, deep+1);
printf("%s", T-> data);
Func(T-> rchild, deep+1);
if(deep > 1){
printf(")");
}
}
}
}2018年:

c
int Func(int A [], int n){
int *B = (int*)malloc(sizeof(int)*(n+1));
int k;
for(int i = 0; i <= n; i++){
B [i] = 0;
}
for(int i = 0; i < n; i++){
if(A [i] > 0 && A [i] <= n){
B [A[i]] = 1;
}
}
for(k = 1; k <= n; k++){
if(B [k] = 0){
break;
}
}
return k;
}2019年:

c
// 分段 逆置 合并
void Func(NODE *&L){
NODE *p = L,* q = L,*r;
while(q-> next != NULL){
p = p-> next;
q = q-> next;
if(Q-> next != NULL){
q = q-> next;
}
}
q = p-> next;
p-> next = NULL;
while(q != NULL){
r = q-> next;
q-> next = p-> next;
p-> next = q;
p = r;
}
q = p-> next;
p-> next = NULL;
p = L-> next;
while(p != NULL){
r = q-> next;
q-> next = p-> next;
p-> next = q;
p = q-> next;
q = r;
}
}2020年:

c
int Func(int A [], int m, int B [], int n, int C [], int p){
int i = 0, j = 0, k = 0, D;
int D_MIN = MAX_INT;
while(i < m && j < n && k < p){
D = abs(A [i] - B [j]) + abs(A [i] - C [k]) + abs(B [j] - C [k]);
if(D > D_MIN){
D_MIN = D;
}
if(A [i] <= B [j] && A [i] <= C [k]){
i++;
}else if(B [j] <= C [k] && B [j] <= A [i]){
j++;
}else{
k++;
}
}
return D_MIN;
}